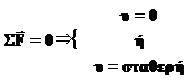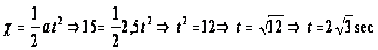Πότε λέμε ότι ένα σώμα κινείται ?
Ένα σώμα λέμε ότι κινείται όταν αλλάζει θέσεις ως προς άλλο σώμα που θεωρείται ακίνητο .
Τι είναι τροχιά και τι διάστημα ενός κινητού ?
Τροχιά ονομάζεται η γραμμή που ενώνει τα σημεία από τα οποία διέρχεται το κινητό .
Διάστημα ονομάζεται το μήκος της τροχιάς του κινητού .
Τι είναι η θέση ενός κινητού ?
Είναι ένας αριθμός που μου δείχνει που βρίσκεται το κινητό σε σχέση με την αρχή του άξονα .
Τι μέγεθος είναι η θέση ?
Διανυσματικό
Τι είναι το διάνυσμα θέσης ενός κινητού ?
Είναι ένα διάνυσμα που έχει αρχή , την αρχή του άξονα και τέλος το σημείο που βρίσκεται το κινητό .
Πως συμβολίζεται η θέση ?
Η θέση συμβολίζεται με το χ
Πως συμβολίζεται η μετατόπιση ?
Η μετατόπιση συμβολίζεται με το Δχ
Πως ορίζεται η μετατόπιση ?
Η μετατόπιση ορίζεται Δχ = χτελικο- χαρχικο
Τι μέγεθος είναι η μετατόπιση ?
Διανυσματικό
Πως συμβολίζεται η χρονική στιγμή ?
Η χρονική στιγμή συμβολίζεται με το t
Πως συμβολίζεται το χρονικό διάστημα ?
Το χρονικό διάστημα συμβολίζεται με το Δt
Πως ορίζεται το χρονικό διάστημα ?
Το χρονικό διάστημα ορίζεται με το Δt=tτελικό-tαρχικο
Τι ονομάζεται ευθύγραμμη κίνηση ?
Μια κίνηση λέγεται ευθύγραμμη όταν το κινητό κινείται σε ευθεία γραμμή .
Τι ονομάζεται ομαλή κίνηση ?
Μια κίνηση λέγεται ομαλή όταν το κινητό κινείται με σταθερή ταχύτητα ( μέτρο ) .
Τι ονομάζεται ταχύτητα ενός κινητού στην ευθύγραμμη ομαλή κίνηση ?
Ταχύτητα ενός κινητού ονομάζεται το φυσικό μέγεθος που ισούται με το πηλίκο της μετατόπισης του κινητού σε κάποιο χρόνο , προς το χρόνο αυτό .
Ο τύπος είναι
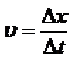
υ : ταχύτητα . Δχ : Μετατόπιση Δt : χρόνος .
Μονάδες ταχύτητας .
Από τον τύπο
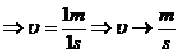
Άλλες μονάδες χιλιόμετρα / h.
Ταχύτητα ενός κινητού δείχνει πόσο γρήγορα κινείται το κινητό
Ευθύγραμμη Κίνηση
Το Χ μου δίνει την θέση Το t μου δίνει χρονική στιγμή
Μεταβολή ενός μεγέθους Α ορίζεται
ΔΑ = Ατελ-Ααρχ
Ρυθμός μεταβολής ενός μεγέθους Α ορίζεται
![clip_image002 [ 3] clip_image002 [ 3]](http://lh4.ggpht.com/_heSFobPCsAM/Sqzs734M_JI/AAAAAAAAB40/MohcZ7e6n94/clip_image0023_thumb.gif?imgmax=800)
Μεταβολή της θέσης ( μετατόπιση )
ΔΧ = Χτελ- Χαρχ
Ρυθμός μεταβολής της θέσης

Μεταβολή του χρόνου ( χρονική διάρκεια )
Δt = tτ-Tα
Ρυθμός μεταβολής της ταχύτητας

Ταχύτητα
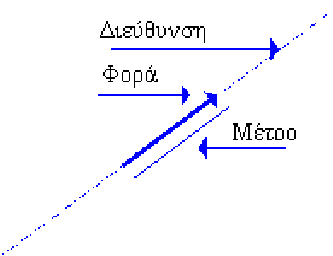
Το μέτρο της ταχύτητας είναι

η διεύθυνση και η φορά της είναι η διεύθυνση και η φορά της μετατόπισης του κινητού .
Mονάδα ταχύτητας στο SI είναι το
Μέση ταχύτητα ονομάζεται το πηλίκο του διαστήματος ς που διανύει ένα κινητό σε ένα ορισμένο χρόνο προς το χρόνο αυτό . Έχει μέτρο
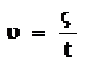
Στιγμιαία ταχύτητα ονομάζεται το φυσικό διανυσματικό μέγεθος που έχει μέτρο
με φορά και διεύθυνση τη φορά και διεύθυνση της κίνησης .
Επιτάχυνση ονομάζεται το φυσικό διανυσματικό μέγεθος που εκφράζεται με το πηλίκο , της μεταβολής της ταχύτητας Δ
Έχει μέτρο
διεύθυνση τη διεύθυνση της κίνησης
φορά τη φορά της κίνησης αν η ταχύτητα αυξάνεται και αντίθετη αν η ταχύτητα μειώνεται .
Μονάδα επιτάχυνσης στο SI είναι το
Στιγμιαία επιτάχυνση ονομάζεται το φυσικό διανυσματικό μέγεθος με μέτρο
διεύθυνση τη διεύθυνση της κίνησης
φορά τη φορά της κίνησης αν η ταχύτητα αυξάνεται και αντίθετη αν η ταχύτητα μειώνεται .
Μέση επιτάχυνση ονομάζεται το πηλίκο της μεταβολής της ταχύτητας προς τον αντίστοιχο χρόνο για μεγάλες χρονικές μεταβολές .
Έχει μέτρο
διεύθυνση τη διεύθυνση της κίνησης
φορά τη φορά της κίνησης αν η ταχύτητα αυξάνεται και αντίθετη αν η ταχύτητα μειώνεται .
Β . Ειδη Ευθυγραμμων Κινησεων
1. Ευθύγραμμη ομαλή κίνηση ονομάζεται η κίνηση που κάνει ένα κινητό όταν αυτό κινείται σε ευθεία τροχιά και το διάνυσμα της ταχύτητας είναι σταθερό . ( σε ίσους χρόνους διανύει ίσα διαστήματα . )| Τύπος | Διάγραμμα | Παρατηρήσεις | |||
α = 0 |  | ||||
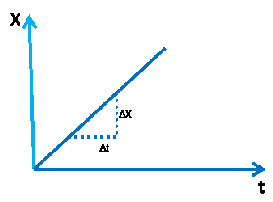
| υ = σταθερή | 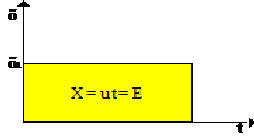 | Το εμβαδόν του σχήματος δίνει τη μετατόπιση Δ X. | |||
| Χ = υ t |
| Η κλίση της ευθείας δίνει την ταχύτητα . |
Να αποδειχτεί ο τύπος της θέσης στην Ε.Ο.Κ
Απόδειξη
Έστω ένα κινητό εκτελεί Ε.Ο.Κ , σύμφωνα με τον ορισμό της ταχύτητας ισχύει :
2. Ευθύγραμμη ομαλά μεταβαλλόμενη ονομάζεται η κίνηση που κάνει ένα κινητό όταν η τροχιά του είναι ευθεία γραμμή και ο ρυθμός μεταβολής της ταχύτητας είναι σταθερός , δηλαδή όταν η επιτάχυνση είναι σταθερή .
3. α. Ευθύγραμμη ομαλά επιταχυνόμενη κίνηση είναι η κίνηση κατά την οποία η ταχύτητα του κινητού διαρκώς αυξάνεται με σταθερό ρυθμό ( α = σταθ . και α > 0) .
| Τύπος | Διάγραμμα | Παρατηρήσεις |
| α = σταθ . ( > 0) | ||
| υ = υο + α t | 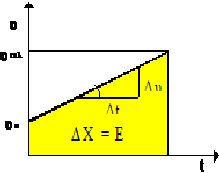 | Το εμβαδόν δίνει τη μετατόπιση ΔΧ Η κλίση της ευθεία δίνει την επιτάχυνση |
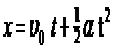 | 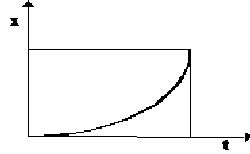 | Τμήμα παραβολής που " ανοίγει " προς τα πάνω . |
| Τύπος | Διάγραμμα | Παρατηρήσεις | ||||||||||
| α = σταθ . ( < 0) | ||||||||||||
| υ = υο - α t | 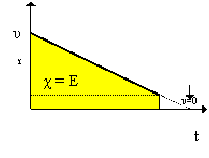 | Το εμβαδόν δίνει τη μετατόπιση Η κλίση της ευθείας δίνει την επιβράδυνση | ||||||||||
| Τμήμα παραβολής που " ανοίγει " προς τα κάτω . |
 |
Απ . Θεωρώ σώμα μάζας m το οποίο έχει αρχική ταχύτητα υο και για χρόνο t επιταχύνεται με επιτάχυνση α και αποκτάει τελική ταχύτητα υ . Τότε σύμφωνα με τον ορισμό της επιτάχυνσης έχουμε :
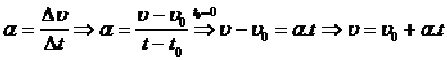
Το πιο πάνω σώμα σε χρόνο t θα μετατοπιστεί κατά χ άρα
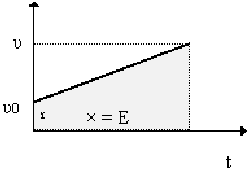
Το εμβαδόν δίνει τη μετατόπιση χ
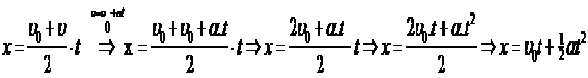
Να βρεθεί ο ολικός χρόνος κίνησης ( tολ) και το μέγιστο
διανυόμενο διάστημα ( Smax) στην ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση .
|

Απ . Θεωρώ σώμα μάζας m με αρχική ταχύτητα υο που επιβραδύνεται με επιβράδυνση α . Μετά από χρόνο tολ το σώμα θα σταματήσει αφού διανύσει διάστημα Smax και τότε θα είναι υτελ= 0 .
Άρα αφού
υτελ= υο -αt
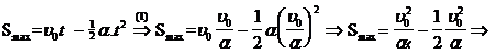
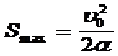
Ένα σώμα που αρχικά ηρεμεί επιταχύνεται με α1= 2 m / s2 για χρόνο t1= 10s . Στη συνέχεια για χρόνο t2= 10s κινείται με σταθερή ταχύτητα και στη συνέχεια επιβραδύνεται με επιβράδυνση α3= 4 m / s2 μέχρι να σταματήσει . Να βρεθούν το συνολικό διάστημα που διάνυσε το κινητό , τη μέση ταχύτητα του και να γίνουν τα διαγράμματα α -t , υ -t , s-t .
Δυο σώματα Α και Β βρίσκονται σε απόσταση 56m και κινούνται με αντίθετες φορές . Το σώμα Α ξεκινάει με αρχική ταχύτητα υ1= 8m / s και επιτάχυνση α1= 2m / s2, ενώ μετά από χρόνο t = 2s ξεκινάει και το σώμα Β χωρίς αρχική ταχύτητα και με επιτάχυνση α2= 4m / s2. Να βρεθεί πότε θα συναντηθούν από τη στιγμή που ξεκινάει το Α σώμα και σε ποία απόσταση από την αρχική θέση του Α θα συναντηθούν ? Τι ταχύτητες θα έχουν τότε τα δύο σώματα ?
Α Χ1 Γ Χ2 ΒΈστω ότι τα δυο σώματα θα συναντηθούν στο σημείο Γ
Το πρώτο θα έχει διανύσει διάστημα
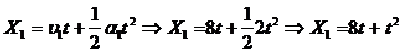 ( 1 )
( 1 ) Το δεύτερο θα έχει διανύσει διάστημα
ΠΑΡΑΤΗΡΗΣΗ :
θέτω t -2 γιατί το δεύτερο κινητό ξεκινάει δύο δευτερόλεπτα αργότερα.
Επίσης θα ισχύει Χ = Χ1+ Χ2 Αντικαθιστώντας την (1) και (2) έχω
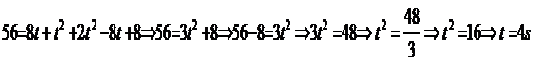
Για να βρω την απόσταση από το σημείο Α που θα συναντηθούν στο χ1 θέτω t = 4 άρα
υ1= υ1+ α1t = 8 2,4 = 16m / s
υ2= Α2( t- 2) = 4.2 = 8m / s
ΑΣΚΗΣΕΙΣ
1) Όχημα που κινείται σε ευθύγραμμο δρόμο με ταχύτητα 10 m / sec επιταχύνεται ομαλά και μετά από 50 m έχει ταχύτητα 30 m / sec . Να βρείτε την επιτάχυνση α και τον χρόνο της κίνησης .
( Απ: α = 8 m/sec2 , t = 2,5 sec )
2) Ένα σώμα που ξεκινάει από την ηρεμία κινείται ευθύγραμμα και στη διάρκεια του 1ου δευτερολέπτου διανύει διαστημα 1 m. Πόσο διάστημα διατρέχει μέσα σε χρόνο t = 2 min ? Πόσο διάστημα θα διατρέξει στη διάρκεια του 12ου δευτερόλεπτου και τι ταχύτητα θα έχει στο τέλος του ίδιου δευτερολέπτου ?
( Απ: S = 14,4 χιλιομέτρων , S12 = 23 m , υ = 24 m / sec )
3) Ένα σώμα που αρχικά ηρεμεί επιταχύνεται με α1 = 2 m/s2 για χρόνο t1 = 10 sec . Στη συνέχεια για χρόνο t2 = 10 sec κινείται με σταθερή ταχύτητα και στη συνέχεια επιβραδύνεται με α2 επιβράδυνση = 4 m/s2 μέχρι να σταματήσει . Να βρεθούν το συνολικό διάστημα που διάνυσε το κινητό , τη μέση ταχύτητα του και να γίνουν τα διαγράμματα α -t , υ -t , s-t .
( Απ: Sολ = 350 m )
4) Δίνεται το διάγραμμα υ-t του σχήματος . Να γίνουν τα διαγράμματα α -t και χ -t .
|
6) Ένα όχημα που κινείται με σταθερή ταχύτητα υ1 = 26 m / sec περνάει τη χρονική στιγμή t = 0 απ ' το σημείο Α . το Την ίδια στιγμή ξεκινάει απ ' σημείο Α δεύτερο όχημα κινούμενο κατά την ίδια φορά με επιτάχυνση α = 2 m/s2. Να βρείτε σε ποιές χρονικές στιγμές η απόσταση των δύο οχημάτων είναι 120 μ. Να κάνετε σε κοινό διάγραμμα τις γραφικές παραστάσεις του διαστήματος με το χρόνο και για τα δύο οχήματα και να δικαιολογήσετε τις τρεις λύσεις από το διάγραμμα .
( Απ: t1 = 6 sec , t2 = 20 sec , t3 = 30 sec)
![clip_image001 [ 5] clip_image001 [ 5]](http://lh5.ggpht.com/_heSFobPCsAM/S-nBQRLSgEI/AAAAAAAADnc/rU0D5M0_SJA/clip_image001%5B5%5D_thumb%5B2%5D.gif?imgmax=800)